可压缩流动和可压缩多相流的数值方法研究领域十分广阔,近几十年来取得了重大成就。然而,由于它适用问题广泛,所以目前仍旧是一个热门的研究话题。最通用的两相可压缩流模型称为7方程模型(1d),该模型考虑了每相的密度、动量、内能、压力、质量分数(10个未知数)。每个相的状态方程与ρ, p, e和质量分数的约束有关,留下了7个未知数。7方程模型可被进一步简化为考虑单一压力的6方程模型以及仅考虑混合速度的5方程模型。基于压力的可压缩流方法与基于密度的可压缩流方法的二分法是众所周知的,它们各有优缺点。
saurel和lemetayer提出了针对界面、激波和传质问题的多相流总体框架。积鼎科技借由本文提出一种压力基方法对全局连续性方程进行非守恒处理以导出压力方程。
一、数学方程
积鼎科技借由本文提出了一种假设单一压力、速度和温度的四方程可压缩多相流模型。该模型可通过求解单独的温度方程扩展为5方程模型,并使用代数滑移模型扩展为6方程版本。
集合平均模型
以体积分数(αk)表示的相质量守恒方程为:
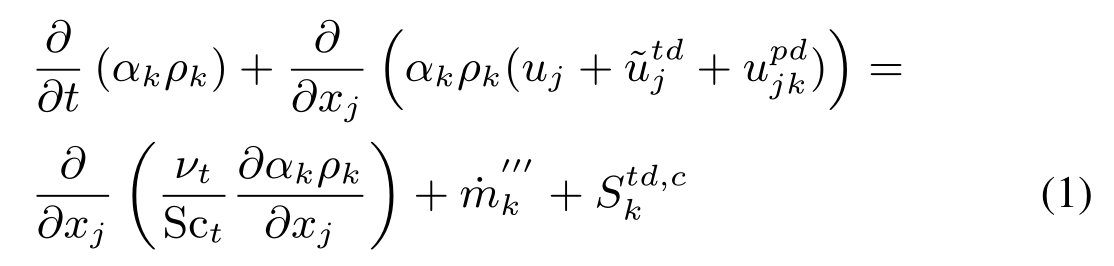
这里引入混合速度平流的物质导数为:

其中ψ是任何平流量,上标m表示平流速度是混合速度。
质量守恒方程可以用质量分数(yk)以物质导数形式重写为:
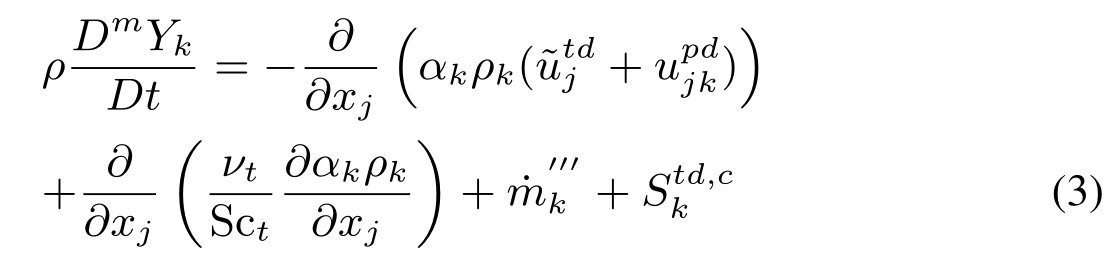
界面跟踪
对于界面跟踪方法,只考虑由level-set函数表示的两相流系统。没有解出相质量守恒方程。level-set方程的演化控制方程如下:
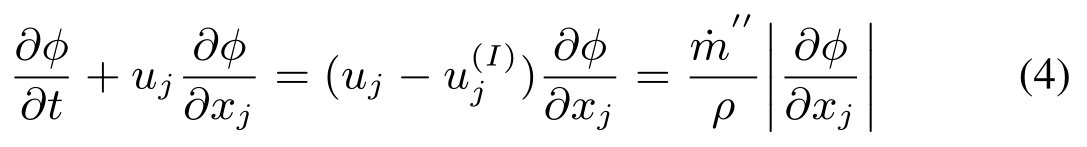
其中φ为到界面的距离,u为界面的速度。平滑heaviside函数hk依赖于距离函数hk = hk(φ)。hk的物质导数为:
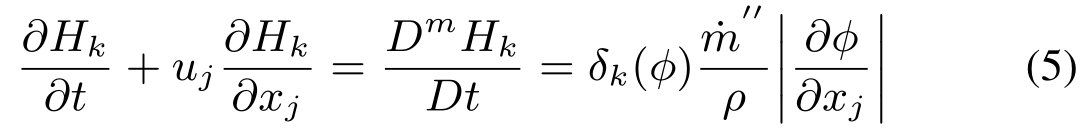
其中δk(φ)为选择界面的光滑狄拉克函数。
mixture动量方程
mixture动量方程如下:
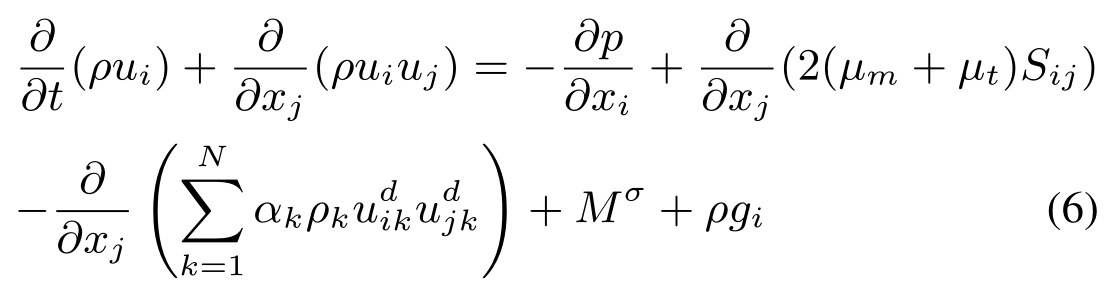
其中一个关键假设是混合粘度模型,该模型考虑了由于滑移引起的粘性动量传递。对于界面跟踪方法,漂移速度项设为零。
mixture温度方程
通过定义显混合焓推导出混合温度方程,其中t0为共同参考温度,cp为混合热容量(假设相热容恒定)。
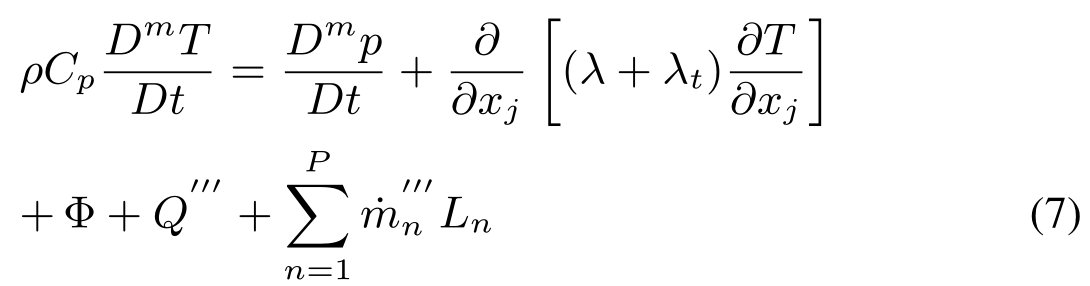
式中φ为动能的粘性耗散,最后一项为p个不同分量发生相变时的潜热贡献,而混合速度对t平流的物质导数可以简化为:
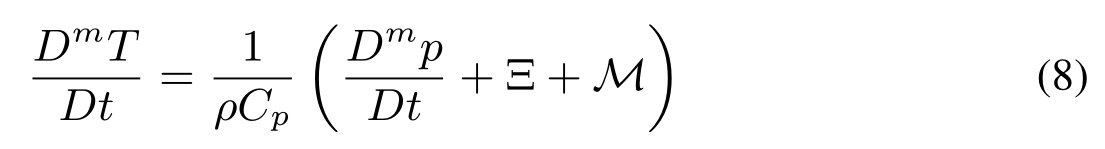
系综平均系统压力方程的发展
导出可压缩多相流压力方程的起点是非守恒形式的mixture连续方程:

取ρ = ρ(p, t, yk)我们可以将上述方程展开为基于独立未知量的线性化,如下:
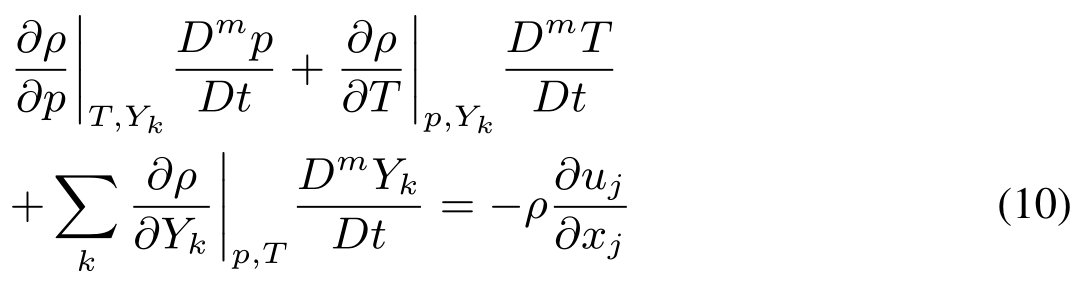
为了评估约束导数,我们从相对于相密度和质量分数的密度定义开始:

式中ρk = ρk(p, t)。在恒定(t, yk)下求ρ对p的导数:
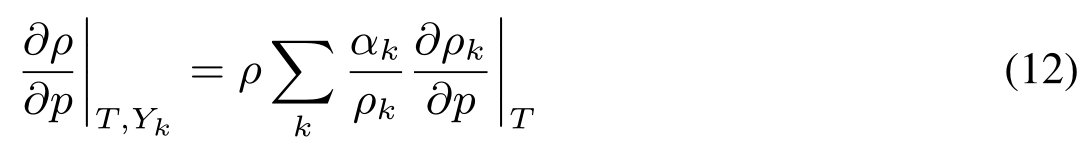
这是等温混合声速。同样地,常数(p, yk)处的导数可以写成:
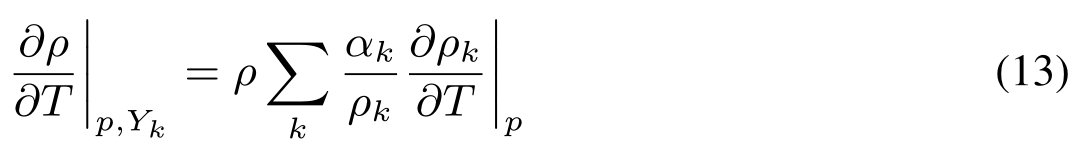
恒定(p, t)时密度对yk的导数为:

将方程(12)-(14)、方程(8)、方程(3)代入方程(10),得到:
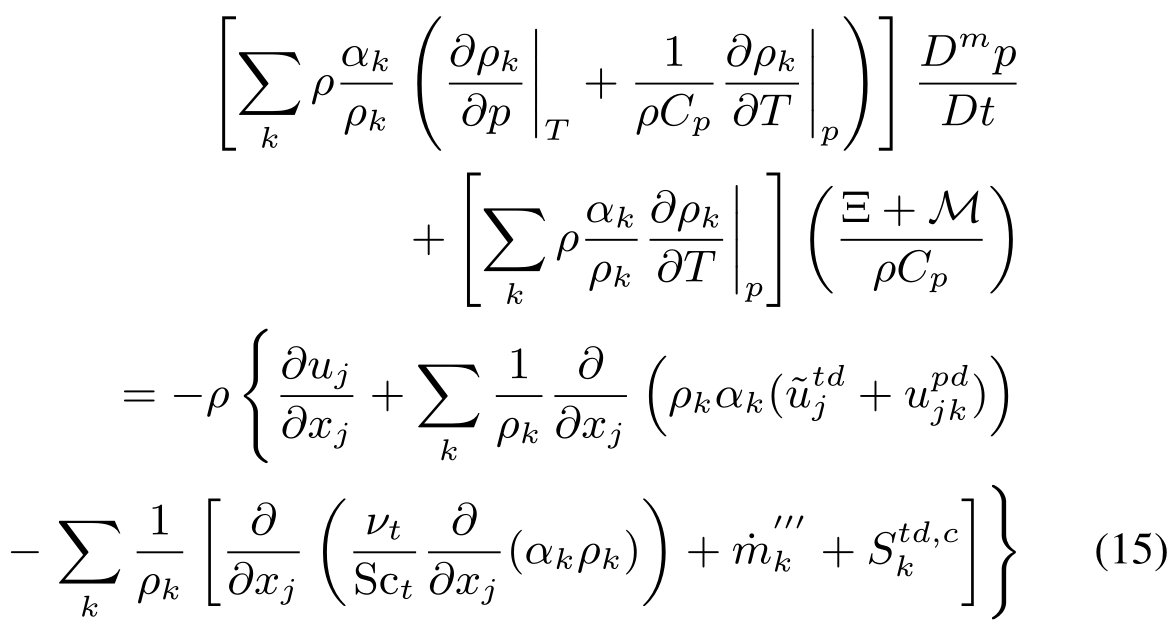
这是n相可压缩流压力方程的最终形式。
单相流的限制
对于可压缩的单相流,方程(15)可简化为:
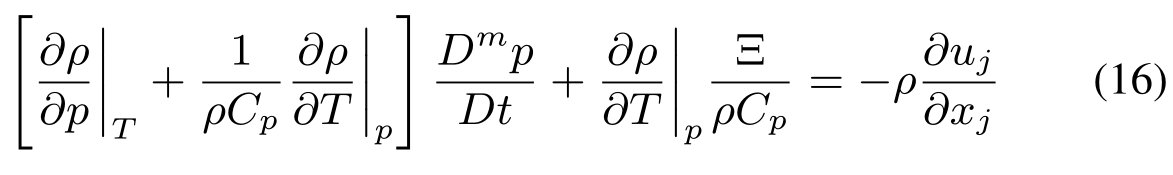
由于理想气体满足状态方程p = ρrt,所以可以导出:
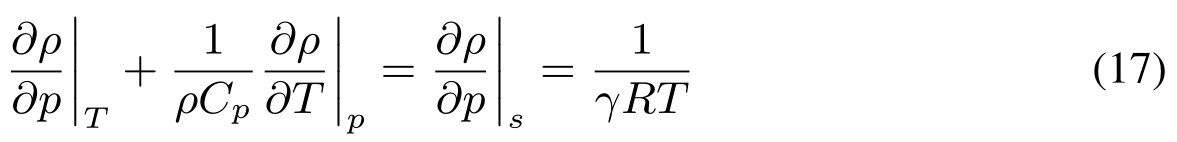
利用cp−cv = r和cp/cv = γ的关系。对于理想气体等熵流动,将方程简化为声波方程。
不可压缩多相流的限制
在不可压缩流动的极限下,由于ρk不是(p, t)的函数,所以可得:
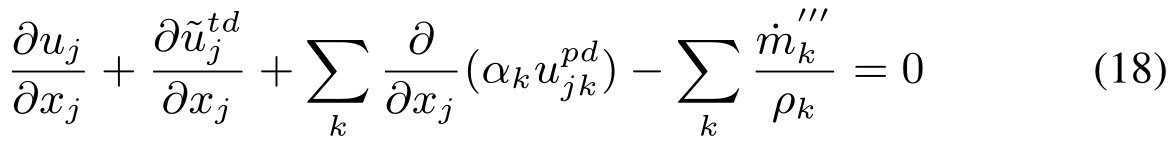
在不存在相间滑移和相变的情况下,这给出了速度场的无散度条件。
界面跟踪的压力方程
对于level-set界面跟踪方法,我们使用hk作为主要变量,线性化连续性方程:
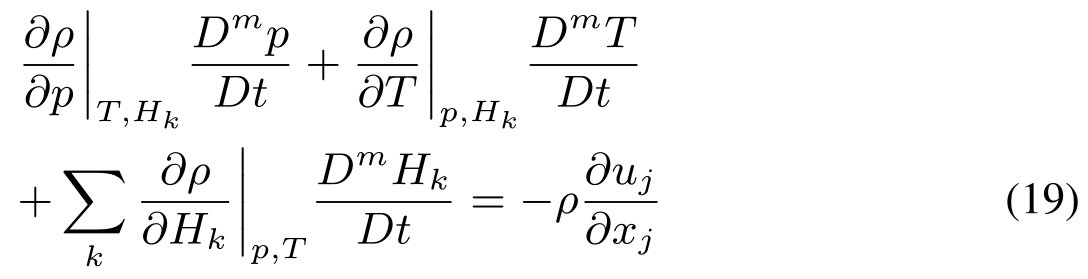
利用方程(5)的定义,可得:
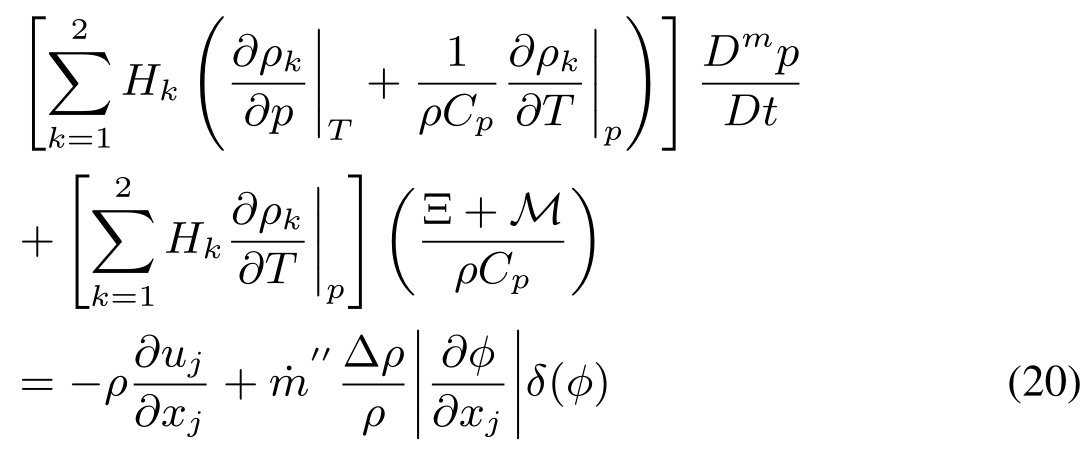
方程(20)中的最后一项为由于相变导致的源项。需要注意的是,流体体积模量的体积加权求和并不能得到由系综平均方程得到的wallis声速。
利用这一公式,提出一种处理不可压缩和可压缩多相流的综合平均和界面跟踪的单一方法。非守恒方程的优点在于它是不可压缩level-set方法的自然推广,而不可压缩level-set方法本身就是非守恒的。这种方法不受接触不连续点附近伪压力振荡的影响。方程(15)和(20)的右侧表示不可压缩项对方程的贡献,而可压缩项对方程贡献置于左侧。此外,该方法还提出了流体的正确体积模量(恒压和恒温的组合),可用于使用等温或等熵导数的压力基方法。其他现象如体加热和相变的影响也被考虑在内。
二、数值离散化
该模型被实现到积鼎virtualflow软件中。virtualflow是一个专门用于多相流建模的有限体积cfd求解器。除压力方程采用一阶迎风外,所有方程的对流项均采用hlpa格式离散化,对非定常问题采用一阶欧拉时间步进。
三、验证
单相流joukowsky问题
这里给出阀门突然关闭的joukowsky问题。问题由(图1)一个充满长度为l = 1m的水域组成,该区域具有固定的压力边界,压力为p0 = 1bar。初始化流速为v0 = 0.0666m/s。根据modified tait状态方程,水的密度为ρ = 1000 kg/(m^3),声速为c = 1481.47m/s。根据理论解,期望压力比为(p0 ρcv0)/p0 = 2。
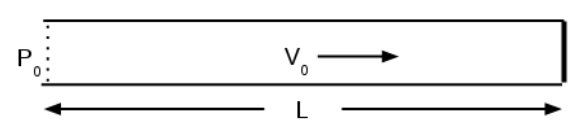
图1:joukowsky问题的草图
区域封闭端(阀)处的压力演化如图2所示,并与解析解进行了对比。在这种情况下,计算域被离散为100个控制体。压力峰值预测准确,但随着时间的推移,由于数值扩散,波形变得模糊。精细化网格(200和400单元)的结果如图3所示,表明它们逐步收敛。
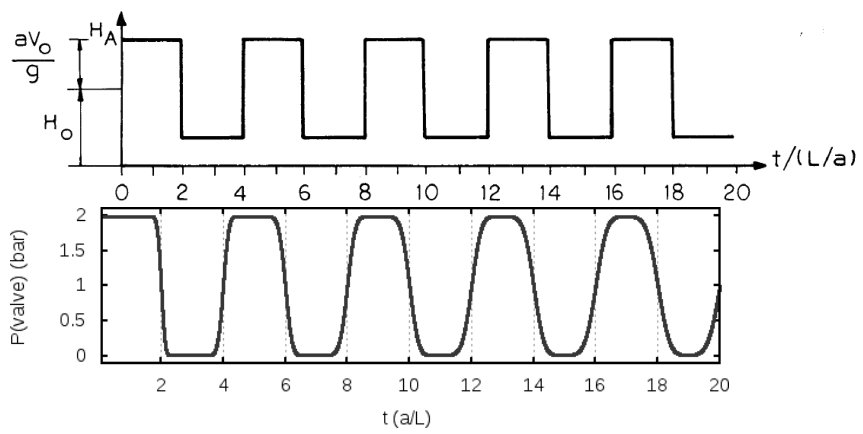
图2:阀门处压力演化对比图
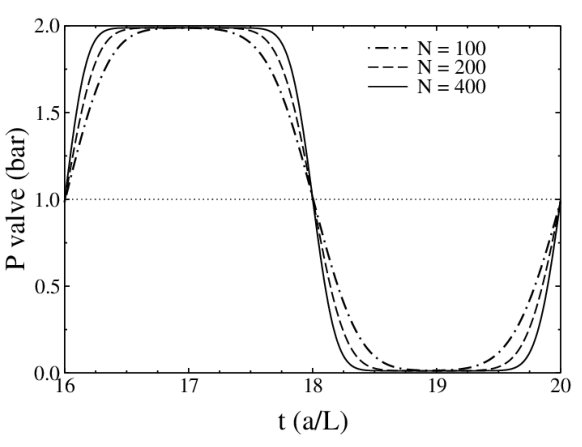
图3:随着网格细化,最后周期内阀门压力变化情况
多相流
这里介绍了该方法在界面流和混合流中的应用。在这两种情况下,结果已与完善的解析解进行了对比。
两相混合物中的声速
为了验证该模型对不同气液混合物的声速预测是否正确,我们初始化了一个长度为0.1 m的一维计算域,其中气体的体积分数分别为1、0.97、0.5、0.1、0,范围从纯气体到纯液体。在计算域的一端设置一个振幅为1000 pa的初始压力脉冲,测量信号到达另一端的时间。使用64个控制体对计算域进行离散化。气相被认为是蒸汽,并被建模为理想气体,其分子量为18 g/mol,热容比为1.2675。用modified tait状态方程对液体进行建模。系统压力设置为1bar,温度初始化为400k。
多相混合物中的声速由wallis声速给出,为:

在所有情况下,远端的压力信号如图4所示。到达速度最快的是纯水,其次是纯空气,根据方程(21)的预测,之后依次到达的是体积分数分别为0.97、0.1和0.5的工况。将数值结果计算的声速与表1中的解析值进行比较。结果与分析值吻合良好(在3%以内)。
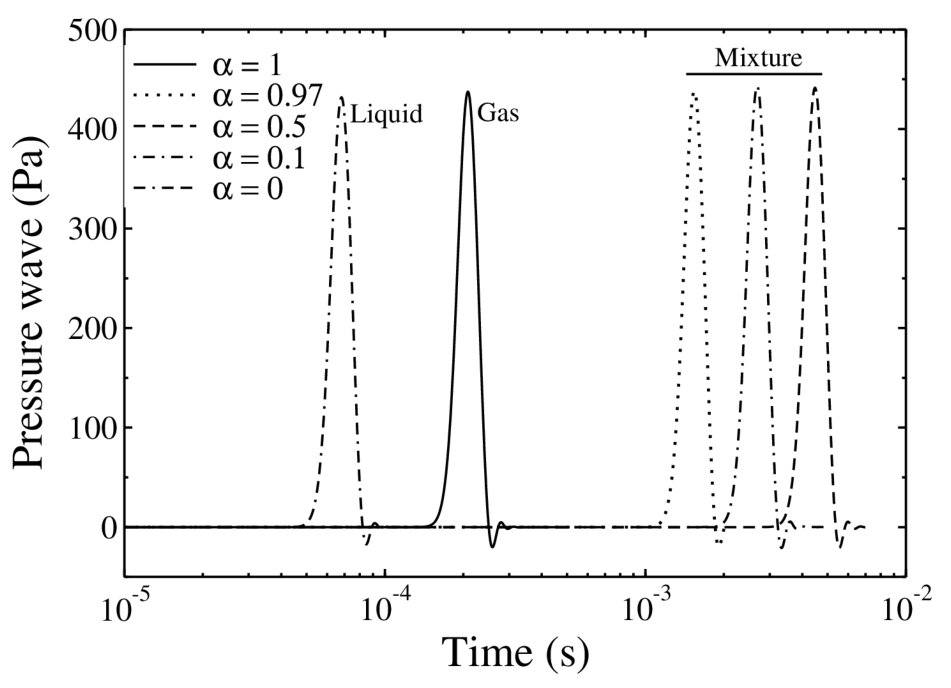
图4:到达远端的压力信号
表1:混合声速分析结果对比
本文模拟了入射压力波在空气-水界面上的传播和反射,即:(a)压力波从空气侧入射,(b)压力波从水侧到达。透射和反射系数由声阻抗给出:
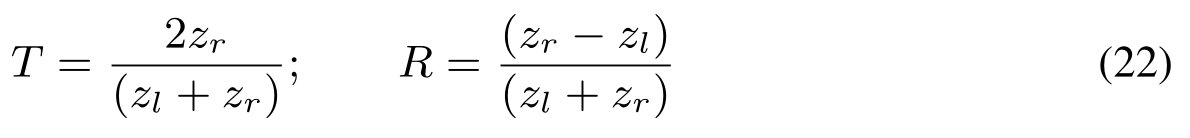
其中z = ρc为声阻抗,下标l和r表示左(入射)和右流体。图5给出了问题描述,其中空气被建模为分子量为28 g/mol,热容量比为1.4的理想气体,水的模型使用modified tait状态方程。
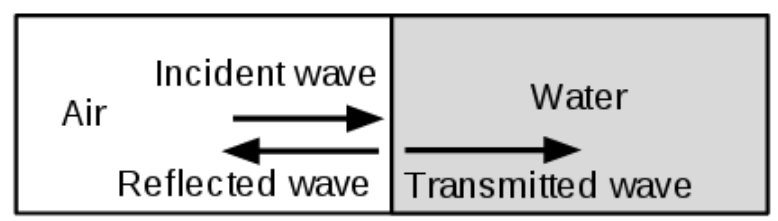
图5:声波透射与反射问题示意图
区域尺寸设为1 m,空气-水界面位于中心。系统压力设置为1bar,温度初始化为300k。振幅为1000 pa的压力脉冲初始化在距离空气或水相界面0.45 m处。本算例采用level-set界面跟踪方法。
解析透射和反射系数如表2所示,并给出了相应的数值结果。这个问题很有趣,因为在空气-水的情况下,反射波的振幅与入射波的振幅相同,而透射波的振幅被放大了2倍。在波来自高阻抗流体(水-空气)的情况下,反射波改变了相位,几乎没有传输任何东西。可见,可压缩界面流动模型能够较准确地再现这种效应。不同波的压力信号如图6所示。
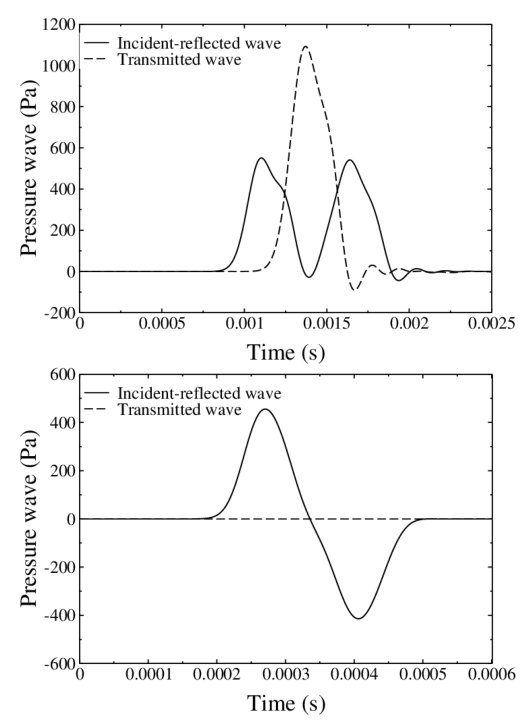
图6:入射波、反射波和透射波的压力信号,上图为空气-水,下图为水-空气。
表2:解析结果与数值结果的比较

四、应用
饱和系统的压力传播
上一节提出的问题被扩展到包括1bar时蒸汽和水之间的传质。温度初始化为饱和温度372.756 k。潜热规定为2.2 mj。选择蒸汽初始体积分数= 0.5的情况。采用基于ranz-marshall相关的分散相传质模型。传质速率(kg/(m^3))为:
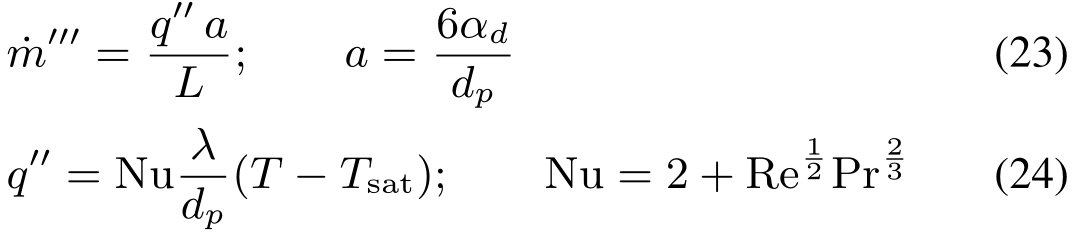
本文中的数值模拟不考虑相间滑移。气泡/液滴直径通过直接输入来确定。通过指定更低的dp值,系统可以被迫进入相平衡状态。这里模拟了三个不同的工况,即20毫米、2毫米和20微米。
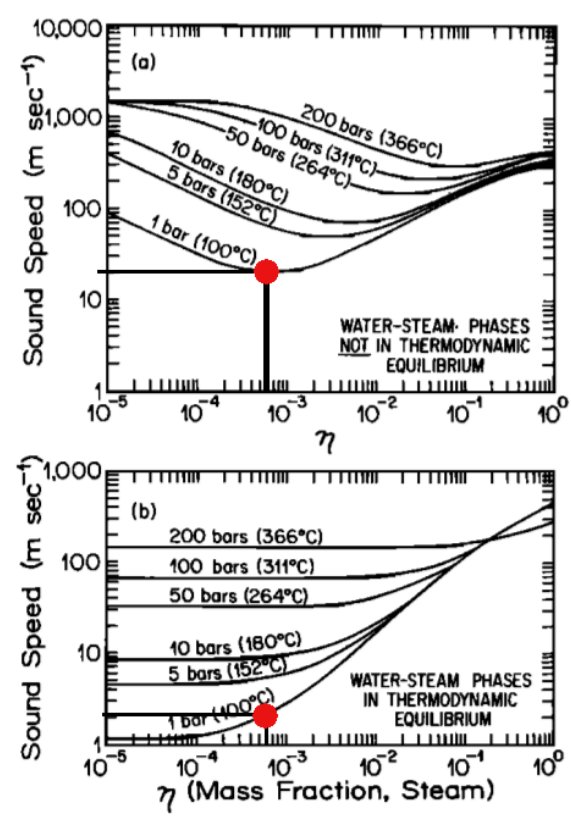
图7:蒸汽-水饱和系统声速变化
饱和系统的声速如图7所示。可以看出,对于1 bar的系统,声速可以低至1 m/s。这里模拟的情况用红点表示。
三种情况下远端压力信号如图8所示。对于较大的气泡/液滴直径,声速几乎不受影响(≈21 m/s),接近图7所示的数据。当dp = 20微米时,压力信号衰减明显,到达远端需要更长的时间。声速估计为1.96 m/s,这与图7中水-蒸汽热力学平衡的数据非常接近。
图8:饱和蒸汽-水系统到达计算域远端的压力信号
喷嘴的临界流动
作为可压缩多相流模型的另一个应用,使用上一节描述的传质模型(方程(24))来解决阀门和喷嘴中的临界流动问题。二维平面喷管示意图如图9所示。
图9:喷嘴几何形状
入口条件:p0 = 3mpa, t0 = 507 k,蒸汽体积分数为0.1的饱和蒸汽-水。通过降低出口压力,找到临界流动条件。采用无滑移的可压缩均匀混合模型,模拟了进出口压力比分别为0.7、0.5、0.4和0.3的情况。传质模型的气泡直径设置为100微米。根据水的antoine方程,计算饱和温度作为压力的函数。利用稳态解算器进行仿真,使其收敛。
图10显示了喷嘴内蒸汽体积分数的变化情况。flashing导致体积分数从入口的0.1增加到喷嘴阻塞前的0.7左右。在多相流情况下,声速非线性特性极强的,所谓的声线(黑色轮廓线)并不一定出现在喉部,如图10中较低的两个压强所示。
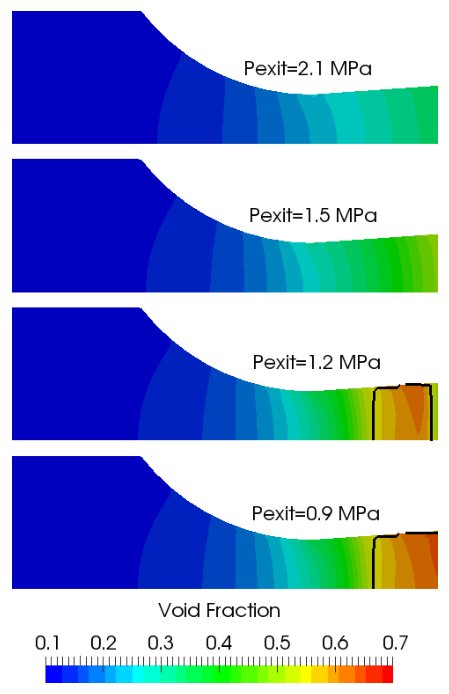
图10:不同出口压力比下的空隙率等高线
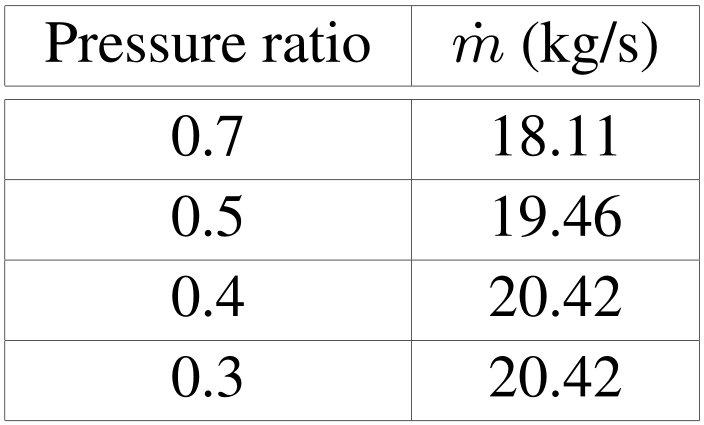
确认临界流量的唯一方法是观察质量流量,并验证它们不会随着出口压力的降低而进一步变化。由表3所示的质量流量可以看出,在压力比为0.3时,流量是临界的。横截面积的宽度为1cm。
表3:通过喷嘴的质量流量。
结论
本文是由积鼎科技提出的一种非保守可压缩多相流模型,该模型是不可压缩多相流模型的自然推广,适用于界面跟踪和系综平均两种方法。用这种单压力、单温度模型精确模拟了几个问题。尽管它比标准的五方程模型更有局限性,但它仍然可以应用于包括冲击和相变在内的广泛问题。